시간, 공간 복잡도(빅오 표기법, 정렬 알고리즘)
가상 메모리 개념을 알게되면서, 개발자가 작업 중 사용하는 메모리와 성능 간의 연관성에 흥미를 가지게 되었고, 실무에서 성능에 영향을 주는 요인들을 조금 더 깊이 이해하고자 학습을 진행하게 되었습니다.
시간 복잡도
알고리즘의 성능을 나타내는 지표로, 입력 크기(n)에 따라 알고리즘이 수행해야 하는 연산 횟수를 의미합니다. 입력 크기가 커질수록 실행 시간이 얼마나 증가하는지를 설명하는 척도로 사용되며, 주로 빅오(Big-O) 표기법*으로 표현합니다.
공간 복잡도
공간 복잡도 또한 알고리즘의 성능을 나타내는 지표로, 알고리즘이 실행되고 종료될때 까지 사용되는 메모리의 양을 입력 크기(n)에 따라 필요한 메모리 사용량을 의미합니다.
입력 크기가 커질수록 얼마만큼의 추가적인 메모리 공간이 필요한지를 측정합니다. 공간 복잡도 또한 빅오(Big-O) 표기법*으로 표현합니다.
최근 컴퓨터의 성능의 발전으로 중요성이 예전 보다 떨어지고 있지만 알고리즘의 중요한 지표로 사용되고 있습니다.
- 고정 공간
- 알고리즘의 실행과 무관한 즉, 알고리즘의 입력값과 무관하게 고정된 메모리 공간
- 코드 저장 공간, 단순 변수 및 상수
- 가변 공간
- 알고리즘의 실행과 관련이 있는 실행중에 사용되는 메모리 공간 문제의 입력값에 따라 가변적으로 사용되는 메모리 공간
- 변수, 함수 호출(재귀 호출), 자료 구조(배열, 리스트 등 동적 크기를 가지는 구조) 등의 요소가 영향을 줌
빅오(Big-O) 표기법
빅오 표기법을 설명하기 앞서 알고리즘 복잡도 표기법에는 세가지가 있습니다.
이 값들은 입력값에 따른 실행 시간의 관계를 나타냅니다.
빅오메가(Big Omega) 표기법
- 최선의 경우(Best Case), 알고리즘의 문제를 가장 빠르게 해결한 경우입니다.
빅세타(Big Theta) 표기법
- 평균적인 경우(Average Case), 알고리즘의 문제를 해결하는 최선, 최악을 기준으로 평균적인 범위입니다.
빅오(Big O) 표기법
- 최악의 경우(Worst Case), 알고리즘의 문제를 가장 오래 걸려 해결한 경우입니다.
왜 빅오 표기법을 사용하는가?
빅오 표기법은 아무리 최악의 상황이라도 이 정도 성능은 반드시 보장한다는 의미로, 시스템 설계나 성능 분석에서 매우 중요한 지표입니다.
쉽게 말해 빅오메가, 빅 세타는 그럴 수 있다는 가정에 가까운 추정이고, 빅오는 무조건 이안에 문제를 해결할 수 있다라는 상한선을 알수있도록 보장하는 정확한 표기이므로 알고리즘의 성능에는 빅오 표기법이 사용됩니다.
성능 순서
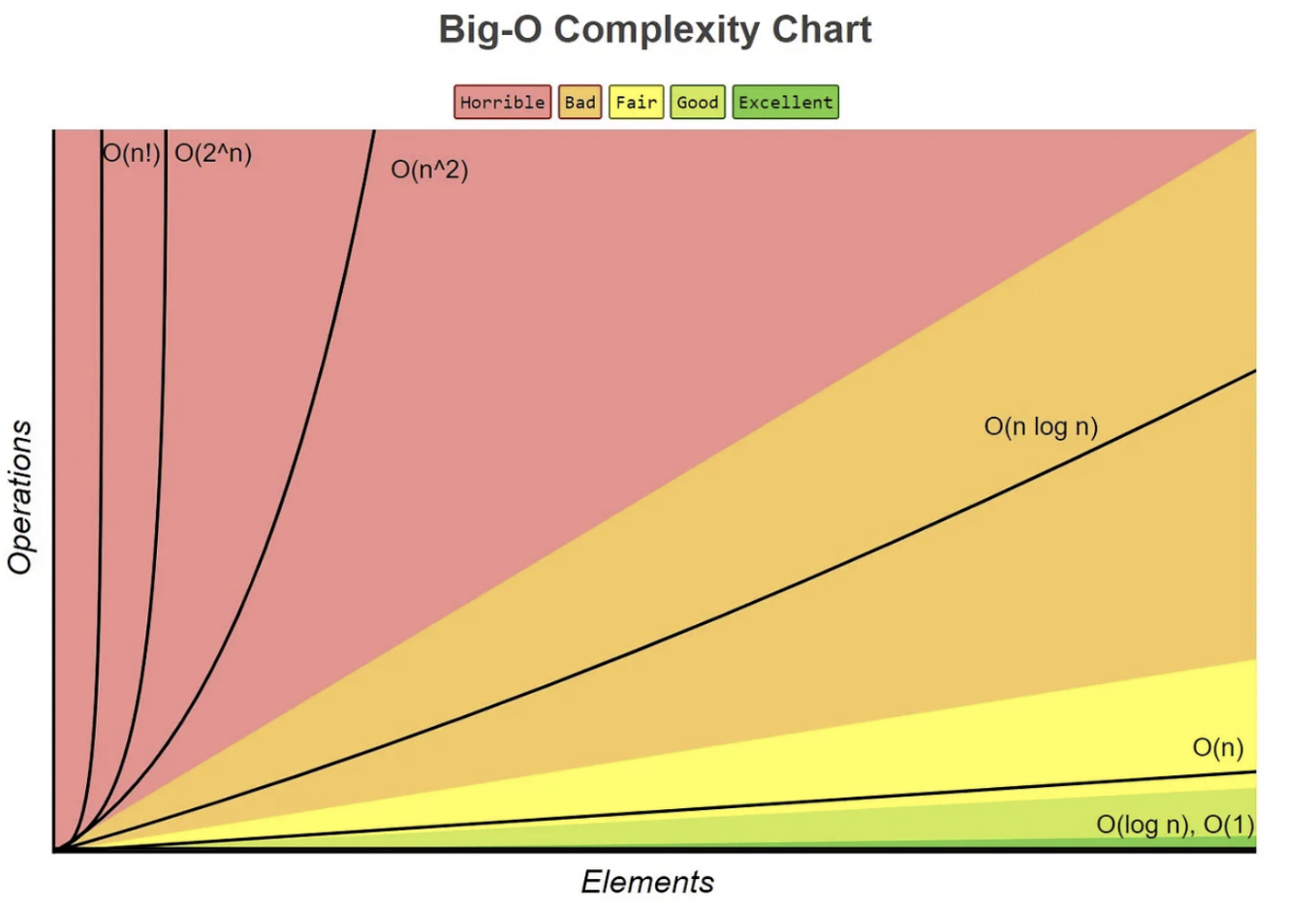
O(1) < O(log n) < O(n) < O(n log n) < O(n2) < O(2n) < O(n!)
O(1)
입력값과 무관하게 고정된 자원을 사용
예: arr[0] 처럼 특정 인덱스 조회
O(log n)
입력값이 커질수록 점차 적은 자원을 사용
예: 이진 탐색(한번 처리할 때마다 절반씩 줄어드는 구조)
O(n)
입력값과 정비례하며 입력값 크기 만큼의 자원을 사용
예: 선형 탐색(for 문, 배열 전체 순회)
O(n log n)
입력값 크기 만큼 log 만큼 자원을 사용
예: 선형 로그 시간(log n 단계로 쪼개거나 정렬하는데 또 다른 과정으로는 n개 만큼 반복하는 구조)
병합 정렬, 퀵 정렬
O(n2)
입력값의 제곱 만큼의 자원을 사용
예: 이차 시간(이중첩 for문 순회)
O(2n)
2의 입력값 크기 만큼의 제곱의 자원을 사용
예 지수 시간(n번중첩 for문 순회)
자원(시간 복잡도: 실행 시간, 공간 복잡도: 실행 공간)
버블 정렬
요소를 반복적으로 비교하고 조건에 맞다면 자리를 스왑하여 정렬을 하는 알고리즘으로, 거품처럼 큰 값이 뒤로 ‘떠오르는’ 모습에서 유래하여 정해졌습니다.
원리는 비교 -> 스왑 -> 비교 -> 스왑… 이런식으로 사이클이 돌아가는 개념입니다.
function bubbleSort(arr: number[]) {
for (let i = 0; i < arr.length - 1; i++) {
for (let j = 0; i < arr.length - 1; j++) {
if (arr[j] > arr[j + 1]) [arr[j], arr[j + 1]] = [arr[j + 1], arr[j]];
}
}
return arr;
}
const arr = [1, 6, 13, 4, 20];
bubbleSort(arr);
과정
1과 6 비교 유지
6과 13 비교 유지
13과 4 비교 스왑
13과 20 비교 그대로
결과 [1,6,4,13,20]
1과 6 비교 유지
6과 4 비교 스왑
6과 13 비교 유지
13과 20 비교 유지
결과 [1,4,6,13,20]
이후는 정렬되어 있으므로 스왑이 없음(단 중단 되지는 않음)
위 예제에서는 2회전으로 결과가 도출되어졌습니다. 이런식으로 비교, 스왑을 반복하며 최종 결과를 도출해내는 구조입니다.
시간 복잡도를 계산해보면, 배열의 요소 개수인 n에 대해 비교를 수행하는 반복문이 다시 n번 실행되므로 전체 반복 횟수는 약 n × n이 되어 O(n²)가 됩니다.
따라서 버블 정렬의 시간 복잡도는 Worst, Best, Average 경우 모두 동일하게 O(n²)이고, 추가 메모리 사용이 없는 제자리 정렬이기 때문에 공간 복잡도는 O(1)입니다.
선택 정렬
배열에서 가장 작은 요소를 선택해서, 정렬되지 않은 부분의 맨 앞자리와 스왑하는 방식의 정렬입니다.
function selectionSort(arr: number[]) {
for (let i = 0; i < arr.length - 1; i++) {
let minIndex = i;
for (let j = i + 1; j < arr.length; j++) {
if (arr[j] < arr[minIndex]) minIndex = j;
}
[arr[i], arr[minIndex]] = [arr[minIndex], arr[i]];
}
return arr;
}
const arr = [1, 6, 13, 4, 20];
selectionSort(arr);
과정
- 가장 최소값 1을 유지
결과 [1, 6, 13, 4, 20]
- 가장 최소값 4를 6과 스왑
결과 [1, 4, 13, 6, 20]
- 가장 최소값 6를 13과 스왑
결과 [1, 4, 6, 13, 20]
이후는 정렬되어 있으므로 스왑이 없음(단 중단 되지는 않음)
위 예제에서는 3회전으로 결과가 도출되어졌습니다. 이런식으로 최소값을 회차마다 앞으로 스왑 시켜 최종 결과를 도출해내는 구조입니다.
시간 복잡도를 계산해보면 배열 요소 개수인 n에 대해 비교를 수행하는 반복문이 다시 n - 1 번 실행 되므로 전체 횟수는 약 n x (n - 1)이 되어 O(n²)가 됩니다.
따라서 선택 정렬의 시간 복잡도는 Worst, Best, Average 경우 모두 동일하게 O(n²)이고, 선택 정렬 또한 제자리 정렬 방법이기 때문에 공간 복잡도는 O(1)입니다.
삽입 정렬
자료 배열의 모든 요소를 앞에서부터 차례대로 이미 정렬된 배열 부분과 비교하여, 자신의 위치를 찾아 삽입하는 방식의 정렬입니다.
맨 앞쪽을 이미 정렬된 배열, 뒤쪽을 정렬되지 않는 배열이라는 기준을 잡음
function insertionSort(arr: number[]) {
for (let i = 1; i < arr.length; i++) {
for (let j = i; j > 0; j--) {
if (arr[j] < arr[j - 1]) {
[arr[j], arr[j - 1]] = [arr[j - 1], arr[j]];
} else {
break;
}
}
}
return arr;
}
const arr = [1, 6, 13, 4, 20];
insertionSort(arr);
과정
- 6과 1 비교 유지
결과 [1, 6, 13, 4, 20]
- 13과 6 비교 유지
결과 [1, 6, 13, 4, 20]
- 4와 13 비교 스왑
- 4와 6 비교 스왑
- 4와 1 비교 유지
결과 [1, 4, 6, 13, 20]
- 20과 13 비교 유지
결과 [1, 4, 6, 13, 20]
시간 복잡도를 계산해보면 배열 요소 개수인 n에 대해 i 번째 요소가 자기 자리를 찾기 위해 j번 비교하고 이동합니다.
따라서 선택 정렬의 시간 복잡도는 Worst, Average 경우 동일하게 O(n²)이고, best에 경우 O(n)이고, 삽입 정렬 또한 제자리 정렬 방법이기 때문에 공간 복잡도는 O(1)입니다.
병합 정렬
배열을 반으로 더이상 나눠지지 않을때까지 나누고, 각 부분을 정렬한 뒤 병합하는 방식의 정렬입니다.
재귀 호출을 이용하여 구현됩니다.
분할 정복*이 사용된 알고리즘입니다.
분할 정복이란?
엄청나게 큰 문제를 조금씩 나눠가면서 작은 단위의 문제를 해결한 뒤 다시 합쳐서 큰 문제를 해결하자는 알고리즘 설계 기법입니다.
// 분할
function mergeSort(arr: number[]) {
if (arr.length <= 1) return arr;
const mid = Math.floor(arr.length / 2);
const leftArr = arr.slice(0, mid);
const rightArr = arr.slice(mid);
const sortedLeft = mergeSort(leftArr);
const sortedRight = mergeSort(rightArr);
return merge(sortedLeft, sortedRight);
}
// 정렬, 병합
function merge(left: number[], right: number[]) {
const result: number[] = [];
while (left.length && right.length) {
if (left[0] < right[0]) {
result.push(left.shift()!);
} else {
result.push(right.shift()!);
}
}
return result.concat(left, right);
}
const arr = [1, 6, 13, 4, 20];
mergeSort(arr);
과정
병합 정렬에는 3가지 단계로 이루어 집니다.
- 분할 단계
- 정복 단계
- 병합 단계
분할 단계
- [1, 6, 13, 4, 20] → [1, 6], [13, 4, 20]
- [1, 6] → [1], [6]
- [13, 4, 20] → [13], [4, 20] → [4], [20]
정복, 병합 단계
- [1], [6] → [1, 6]
- [4], [20] → [4, 20]
- [13], [4, 20] → [4, 13, 20]
- [1, 6], [4, 13, 20] → [1, 4, 6, 13, 20]
결과 [1, 4, 6, 13, 20]
병합 정렬은 배열을 반으로 나누는 분할 작업을 재귀적으로 수행하므로 분할 단계는 O(log n) 번 발생합니다. 각 단계마다 전체 배열을 병합하는 데 O(n) 시간이 걸립니다.
따라서 병합 정렬의 시간 복잡도는 Worst, Average, Best 모두 O(n log n)이고,
재귀 호출을 하므로 평균적으로 O(log n) 만큼의 스택 공간이 사용되고, 병합 단계에서 배열 길이만큼의 추가 배열이 필요하기 때문에, 전체 공간 복잡도는 O(n)입니다.
퀵 정렬
퀵 정렬 또한 병합 정렬과 같은 분할 정복이 사용된 알고리즘입니다.
하나의 기준점을 기준으로 배열을 나누고 왼쪽에는 작은 값, 오른쪽에는 큰 값을 재 배치하는 정렬합니다.
재귀 호출을 이용하여 구현됩니다.
function quickSort (arr: number[]): number[] {
if(arr.length <= 1) return arr;
const pivot = arr[0];
const left = [];
const right = [];
for(let i = 1; i < arr.length; i++) {
if(arr[i] < pivot) {
left.push(arr[i])
} else {
right.push(arr[i])
}
}
const resultLeft = quickSort(left);
const resultRight = quickSort(right);
return resultLeft.concat(pivot, resultRight);
}
const arr = [1, 6, 13, 4, 20];
quickSort(arr);
퀵 정렬의 경우 여러가지 기준점을 잡는것이 가능합니다. 첫번째, 마지막, 중간, 랜덤의 기준점을 잡을수 있는데, 제가 작성한 예제는 첫번째를 기준점으로 잡고 진행하였습니다.
과정
분할 단계
- 배열의 첫번째 값 1 기준 → 왼쪽 [], 오른쪽 [6, 13, 4, 20]
- 배열의 첫번째 값 6 기준 → 왼쪽 [4], 오른쪽 [13, 20]
- 배열의 첫번째 값 13 기준 → 왼쪽 [], 오른쪽 [20]
정복, 연결 단계
- 왼쪽 [] + 기준 [13] + [20] → [13, 20]
- 왼쪽 [4] + 기준 [6] + [13, 20] → [4, 6, 13, 20]
- 왼쪽 [] + 기준 [1] + [4, 6, 13, 20]
결과 [1, 4, 6, 13, 20]
기준값을 기준으로 배열 전체를 분할하므로, 분할 작업이 O(n) 시간에 수행됩니다. 이 분할 작업이 평균적으로 O(log n) 단계 재귀적으로 실행 됩니다.
따라서 퀵 정렬의 시간 복잡도는 Best, Average는 O(n log n)이고, Worst는 기준점이 배열에서 가장 작은값 또는 큰값으로 편향될 시에는 O(n²)입니다.
재귀 호출을 하므로 평균적으로 O(log n) 만큼의 스택 공간이 사용되고, 기준점이 배열에서 가장 작은값 또는 큰값으로 편향될 시에는 O(n)의 추가 배열이 사용되므로, 전체 공간 복잡도는 O(n)입니다.
